🔸 Issue #23: Firefly Algorithm
Plus: Panora startup for connecting llms, latest Paul G. post - Founder Mode, and Jürgen Schmidhuber interview!
🗒️ IN TODAY’S ISSUE
🔸 “Firefly algorithm” from the paper “The Vizier Gaussian Process Bandit Algorithm”
👨🏻💻 “Panora” - build on a single API, cut maintenance time, and keep your teams focused
🧠 “Founder Mode” - Latest Paul Graham blog post
📱 Jürgen Schmidhuber interview at MLST
🔸 Extract: Firefly algorithm
From the paper: “The Vizier Gaussian Process Bandit Algorithm” by Xingyou Song, Qiuyi Zhang, Chansoo Lee, Emily Fertig, Tzu-Kuo Huang, Lior Belenki, Greg Kochanski, Setareh Ariafar, Srinivas Vasudevan, Sagi Perel, Daniel Golovin
Paper Summary: Google Vizier has become a powerhouse in the realm of black-box optimization, having successfully tuned over 70 million objectives at Google. The paper highlights the advancements made in the Vizier Gaussian Process Bandit Algorithm, showcasing its evolution through extensive research and user feedback. This open-source implementation aims to provide a robust and versatile tool for both researchers and practitioners in the field of Bayesian optimization.
At the heart of the Vizier algorithm are several innovative components. It employs a Gaussian Process model with a Matern-5/2 kernel and automatic relevance determination (ARD) to ensure accurate modeling. The algorithm also incorporates sophisticated input and output preprocessing techniques to enhance the performance of the Gaussian Process regression, addressing challenges like outliers and scaling issues effectively.
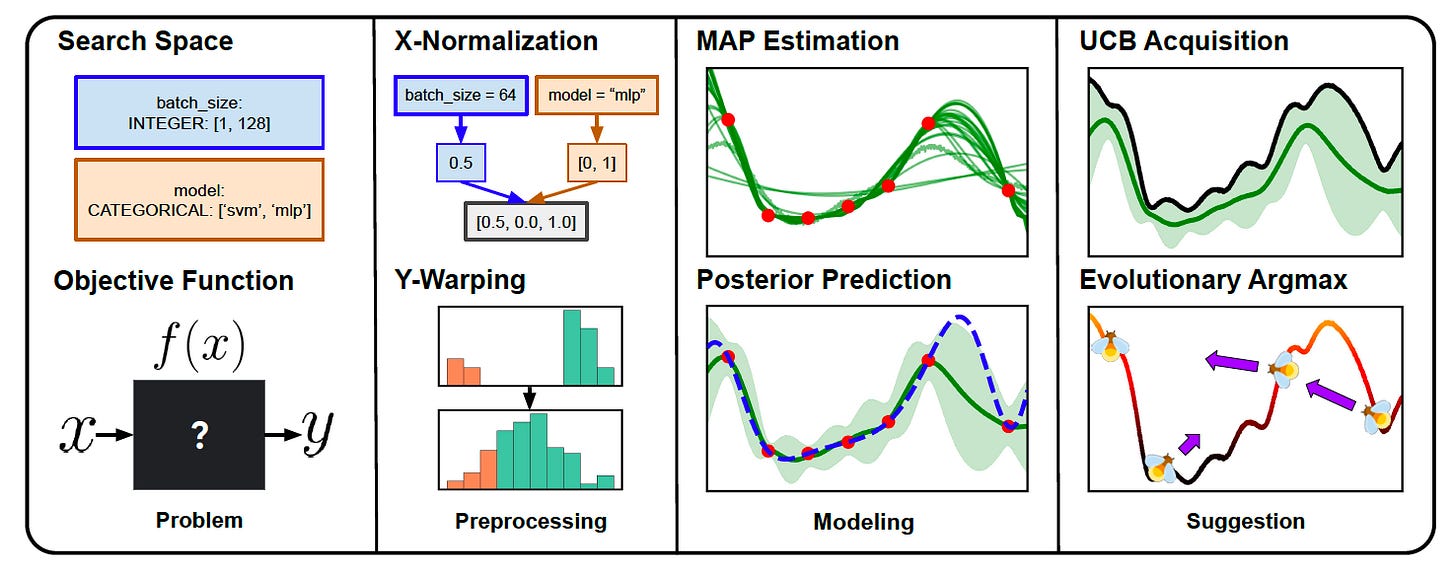
The results indicate that Vizier not only performs well but also adapts seamlessly to different types of optimization tasks, making it a versatile choice for users.
One notable aspect of the Vizier algorithm is its use of a zeroth-order evolutionary acquisition optimizer, which is somewhat unconventional. The authors discuss how this design choice contributes to the algorithm's strengths, particularly in balancing exploration and exploitation during the optimization process.
While the paper focuses on the open-source aspects of Vizier, it acknowledges that the platform supports additional features like contextual bandits and transfer learning. However, these are not the primary focus of the current discussion. Overall, the paper serves as a valuable resource for those looking to leverage the power of Bayesian optimization in their projects.
What is the Firefly Algorithm?
In the realm of computational intelligence, nature continues to inspire innovative solutions to complex problems. One such inspiration comes from the humble firefly, whose bioluminescent signaling has given rise to a powerful optimization technique known as the Firefly Algorithm.
Developed by Xin-She Yang at Cambridge University in 2008, the Firefly Algorithm has quickly gained traction in the field of optimization due to its elegance and effectiveness. This algorithm ingeniously mimics the behavior of fireflies, using their light-based communication as a metaphor for solution quality in optimization problems.
How It Works
At its core, the Firefly Algorithm operates on a population of agents, each representing a potential solution. The brightness of a firefly corresponds to the quality of its solution, with brighter fireflies attracting others. This attraction mechanism is governed by two key principles:
The brightness of a firefly decreases with distance
Fireflies move towards brighter ones
This simple yet effective approach allows the algorithm to balance the exploration of new areas with the exploitation of known good solutions, often leading to convergence towards a global optimum.
Versatility in Application
One of the Firefly Algorithm's most compelling features is its adaptability to various optimization challenges. It has proven particularly effective in handling multimodal and multi-objective problems, making it suitable for a wide range of applications across different industries:
Engineering Design: Optimizing structural designs and antenna configurations
Machine Learning: Enhancing feature selection and parameter tuning
Image Processing: Improving segmentation and compression techniques
Finance: Assisting in credit risk assessment when combined with support vector machines
The following implementation includes the core components of the Firefly Algorithm:
Initialization of fireflies
Calculation of light intensity (fitness)
Movement of fireflies towards brighter ones
Updating the best solution
import numpy as np
import matplotlib.pyplot as plt
class FireflyAlgorithm:
def __init__(self, func, dim, n_fireflies, n_generations, alpha, beta0, gamma):
self.func = func
self.dim = dim
self.n_fireflies = n_fireflies
self.n_generations = n_generations
self.alpha = alpha # Randomization parameter
self.beta0 = beta0 # Attractiveness at distance = 0
self.gamma = gamma # Light absorption coefficient
def initialize_fireflies(self):
return np.random.rand(self.n_fireflies, self.dim)
def calculate_intensity(self, fireflies):
return np.array([self.func(firefly) for firefly in fireflies])
def update_fireflies(self, fireflies, intensity):
new_fireflies = np.copy(fireflies)
for i in range(self.n_fireflies):
for j in range(self.n_fireflies):
if intensity[j] > intensity[i]:
r = np.linalg.norm(fireflies[i] - fireflies[j])
beta = self.beta0 * np.exp(-self.gamma * r**2)
new_fireflies[i] += beta * (fireflies[j] - fireflies[i]) + \
self.alpha * (np.random.rand(self.dim) - 0.5)
return new_fireflies
def optimize(self):
fireflies = self.initialize_fireflies()
best_solution = None
best_intensity = float('-inf')
for _ in range(self.n_generations):
intensity = self.calculate_intensity(fireflies)
fireflies = self.update_fireflies(fireflies, intensity)
gen_best_idx = np.argmax(intensity)
if intensity[gen_best_idx] > best_intensity:
best_solution = fireflies[gen_best_idx]
best_intensity = intensity[gen_best_idx]
return best_solution, best_intensity
# Example usage
def objective_function(x):
return -(x[0]**2 + x[1]**2) # Maximizing negative of sphere function
fa = FireflyAlgorithm(func=objective_function, dim=2, n_fireflies=20, n_generations=50,
alpha=0.5, beta0=1.0, gamma=0.1)
best_solution, best_intensity = fa.optimize()
print(f"Best solution: {best_solution}")
print(f"Best intensity: {best_intensity}")To better understand the algorithm's behavior, you can add a visualization component:
def visualize_fireflies(fireflies, best_solution):
plt.figure(figsize=(10, 8))
plt.scatter(fireflies[:, 0], fireflies[:, 1], c='orange', label='Fireflies')
plt.scatter(best_solution[0], best_solution[1], c='red', s=100, label='Best Solution')
plt.title('Firefly Algorithm Optimization')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
# Add this after the optimization
visualize_fireflies(fa.initialize_fireflies(), best_solution)Current Research and Future Prospects
The algorithm's success has spurred ongoing research into modifications and hybrid approaches, aiming to enhance its performance further. As the field of optimization continues to evolve, the Firefly Algorithm remains a promising tool, poised for innovations that could expand its applicability to even more complex problem domains.
To better understand the Firefly Algorithm's effectiveness, it's worth examining its underlying mechanics in more detail. The algorithm operates iteratively, with each iteration potentially improving the quality of solutions. Here's a more detailed look at its process:
Initialization: A population of fireflies is randomly distributed across the solution space, each representing a potential solution to the optimization problem.
Brightness Evaluation: The algorithm evaluates the "brightness" (fitness) of each firefly based on the objective function of the problem at hand.
Movement: Fireflies move towards brighter ones according to an attraction function. This function typically considers both the distance between fireflies and their relative brightness.
Attractiveness: The attractiveness of a firefly decreases as the distance from the viewing firefly increases. This is modeled using an exponential decay function.
Random Walk: A small random movement is added to each firefly's position to introduce diversity and prevent premature convergence to local optima.
Update and Iteration: After movement, the algorithm re-evaluates the brightness of all fireflies and repeats the process for a set number of iterations or until a stopping criterion is met.
This process allows the algorithm to efficiently explore the solution space while gradually converging towards optimal solutions.
Comparative Advantages
When compared to other nature-inspired algorithms, such as Particle Swarm Optimization (PSO) or Genetic Algorithms (GA), the Firefly Algorithm offers several distinct advantages:
Automatic Subdivision: The algorithm can automatically subdivide the population into subgroups, each of which swarms around a local optimum. This makes it particularly effective for multimodal optimization problems.
Ability to Handle Nonlinear Problems: The algorithm's nonlinear update mechanism allows it to handle highly nonlinear optimization problems effectively.
Flexibility in Tuning: The algorithm offers flexibility in tuning its parameters to balance exploration and exploitation, making it adaptable to a wide range of problem types.
Challenges and Future Directions
Despite its successes, the Firefly Algorithm is not without challenges. Researchers continue to work on addressing some of its limitations:
Parameter Sensitivity: The algorithm's performance can be sensitive to parameter settings, which may require careful tuning for optimal results.
Computational Complexity: For large-scale problems, the algorithm's computational requirements can be significant, prompting research into more efficient implementations.
Convergence Speed: In some cases, the algorithm may converge slowly, especially for high-dimensional problems.
Future research directions include developing adaptive parameter strategies, hybridizing the Firefly Algorithm with other optimization techniques, and exploring its application in emerging fields such as quantum computing and blockchain optimization.
Until next week,
Nino.
👨🏻💻 AI Startup
Panora is shaking up enterprise data access. It offers a universal API for connecting to various SaaS platforms. This open-source tool allows companies to build AI solutions using their internal data.
The key benefit is speed. Panora eliminates months of integration work. It ingests data from multiple sources. Then it provides clean, well-documented APIs. Engineers can query this data easily. They can focus on core product development instead of building integrations.
For AI practitioners, this is a game-changer. It enables quick access to diverse enterprise data. This can lead to more advanced AI systems and agents. Panora is set to accelerate innovation in business process automation and AI-driven decision-making.
🧠 Article
Founder Mode by Paul Graham
Brian Chesky's YC talk revealed a truth:
Conventional wisdom on running large companies often fails founders
"Hire good people and give them room" can be disastrous advice
The Two Modes
Founder mode: An emerging, powerful approach
Manager mode: The traditional method
Founders feel caught between conflicting advice and employee expectations.
Steve Jobs' Example
Annual retreats with 100 key people, regardless of rank
Unconventional, but potentially game-changing
The article suggests that understanding "founder mode" could revolutionize how successful startups are run, potentially leading to even greater innovations in the tech world.



